How EQ Changes Phase | 1 FREE Mastering SECRET You Need to Know!
Quick Answer
Depending on the type of equalization you use, you may or may not alter the phase of various frequencies. When the phase of a signal is altered by equalization, this can have both negative and positive impacts on the quality, enjoyability, and psychoacoustic perception of the signal.
How EQ Changes Phase | 1 FREE Mastering SECRET You Need to Know! In Detail
Phase is a complex topic. It becomes even more complex when we consider how different algorithms are used to create equalizers, and how this ultimately affects the phase of our signal.
Furthermore, to understand this topic fully, we also need to understand why phase matters at all, or how it affects our perception of a sound source.
With that in mind, we’ll discuss a lot of concepts here, including phase relationships and interference , the Fast Fourier Transform algorithm, zero latency, and linear phase equalizers, pre-ringing, and the psychoacoustic effect known as the Haas effect.
We’ll also use analyzers to measure the phase and frequency response of an equalized signal to see how accurate our equalizers are.
If you’re an artist or engineer, and you have a mix that you’d like to hear mastered, send it to us here:
We’ll master it for you and send you a free mastered sample to review.
What is Phase in Audio?
Phase relates to the positioning and timing of sound waves as they relate to one another; when two or more signals are in-phase this is called constructive interference and results in amplification. When two or more signals are out of phase this is called destructive interference, resulting in attenuation.
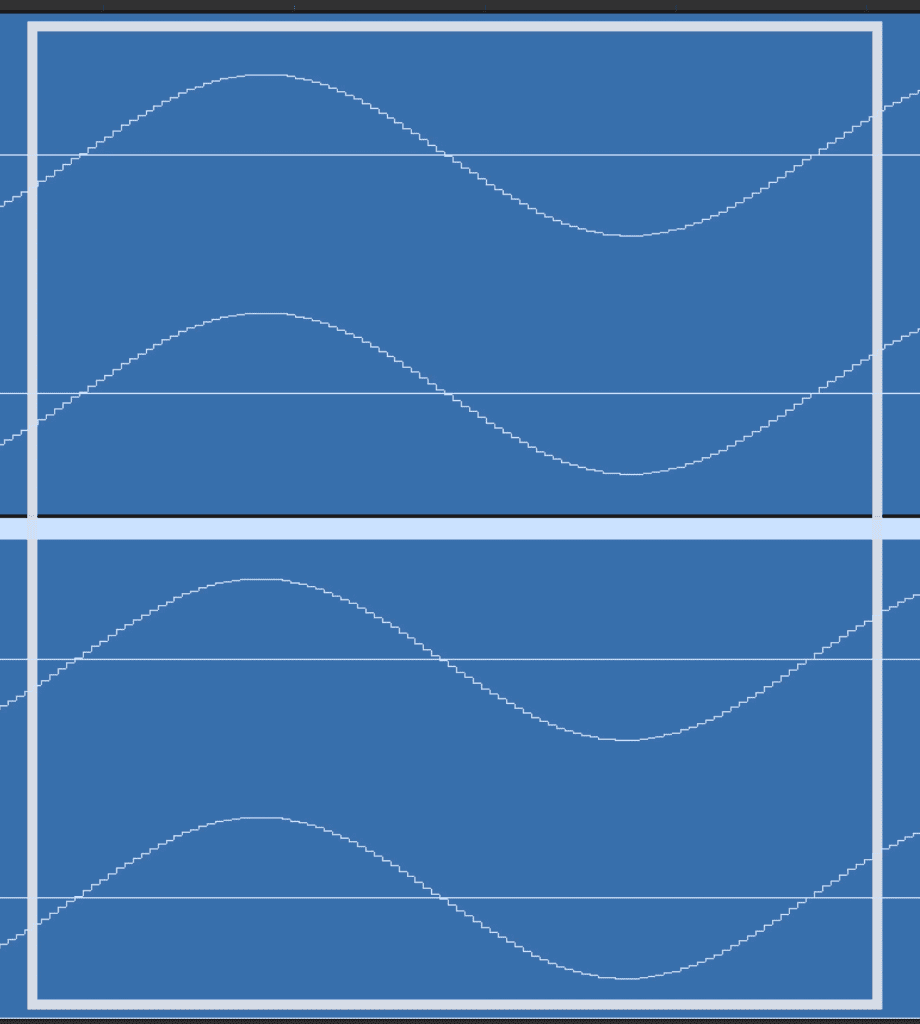
Shown are 2 in phase 500Hz sine waves.
To better understand this concept let’s look at 2 sine waves with the same frequency. When we zoom in on these waveforms, we can see that they match.
In audio terms the peak and troughs of the waves align. When this occurs it’s called being in-phase. It’s also referred to as the phase being at 0 degrees.
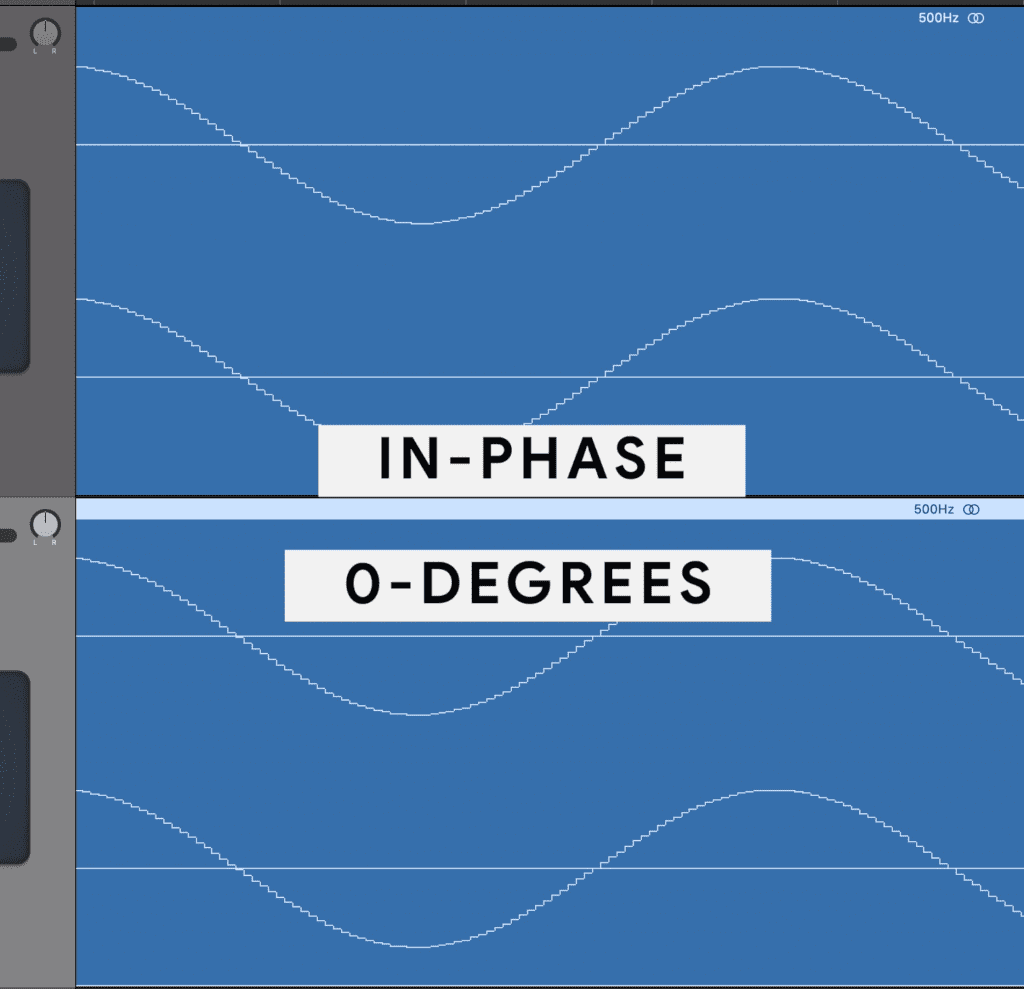
When peaks and troughs are aligned it's called in phase, or 0-degree phase.
If we play these 2 tracks, the signals, being in time with one another, will add to one another - this is called constructive interference.
If we were to drag one of these tracks over, we would see that they are no longer aligned. If we drag it far enough, the peak of one track would align with the trough of another.
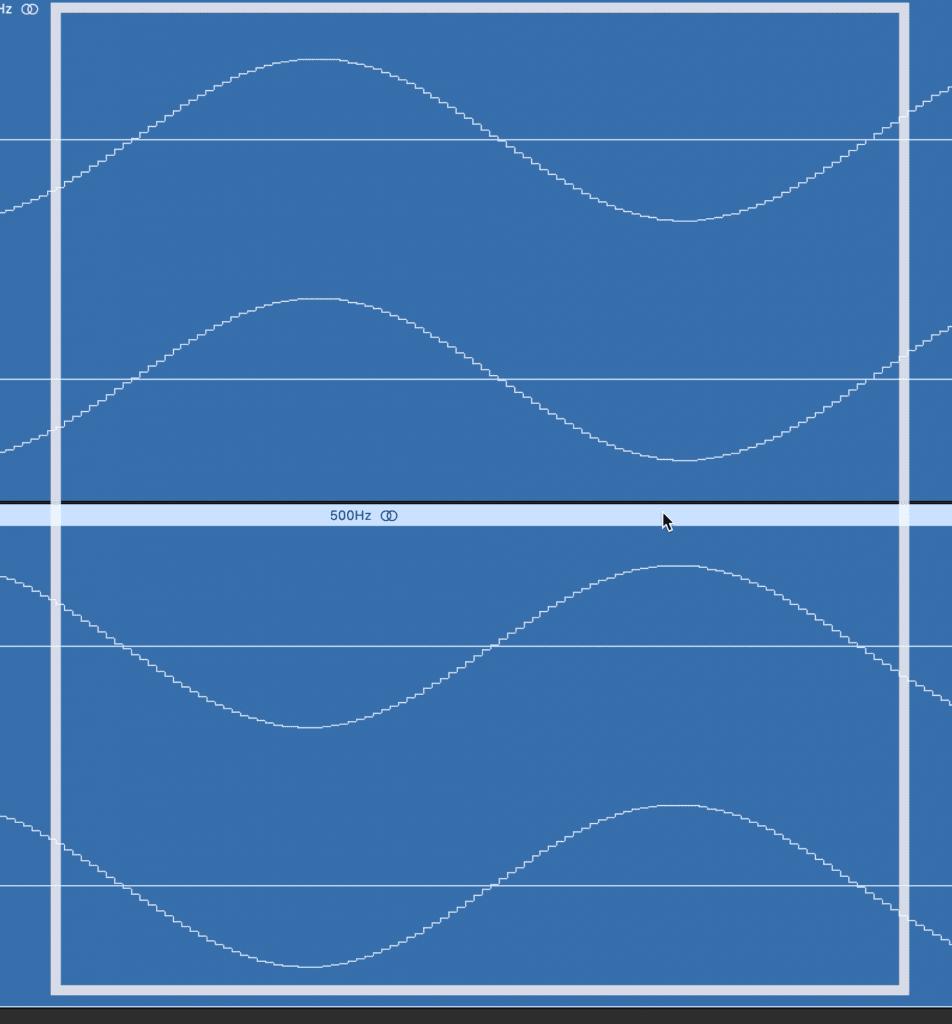
Shown here are 2 out-of-phase sine waves.
When this occurs it’s called being out-of-phase. It’s also referred to as the phase is at 180 degrees.

When waves are out of phase, the peak of one wave aligns with the trough of another.
When we play the track now, the signals, being out of time with one another, will cancel one another out or nullify each other - this is called destructive interference.
Now that we understand these concepts, let’s look at some equalizers to see how they affect the phase of a signal.
If you need some free equalizers, check out this video about them:
How does EQ Change Phase?
When we think about EQ and phase, we often think that using an equalizer causes a shift in a signal’s phase; however, it is through phase cancellation that most equalizers work at all. Any equalizer that is zero-latency will inevitably alter the phase of the signal.
To understand why this is, we need to delve into something called the Fast Fourier Transform. Now, we don’t need to get into the specifics of the algorithm or how it works on a mathematical level, but we do need to know what it means for equalizers.
Essentially, any equalizer that’s created using FFT doesn’t have every frequency represented. Like digital audio in general, the overall signal is broken up into samples.

More equalizers use samples to represent various frequencies. The number of samples used it usually around 4096 samples.
So let’s say an EQ uses 4096 samples. Using the Nyquist Frequency Theorem we know that this means we can have 2048 frequencies. If our session has a 44.1kHz sampling rate, then our available frequency range is 22050Hz.

This means that this EQ can accurately alter a frequency every 10.766 Hz.
Because only 2048 frequencies of this 22050Hz range can be represented, we end up with about 1 band every 10Hz. Each of these bands is referred to as a minimum-phase filter since they each very subtly alter the timing and in turn the phase of the signal.
This is all getting a little confusing so let’s look at the phase of an equalizer using the Bertom EQ Curve Analyzer.
Let’s create a bell filter at 500Hz, and amplify it by 4dB.
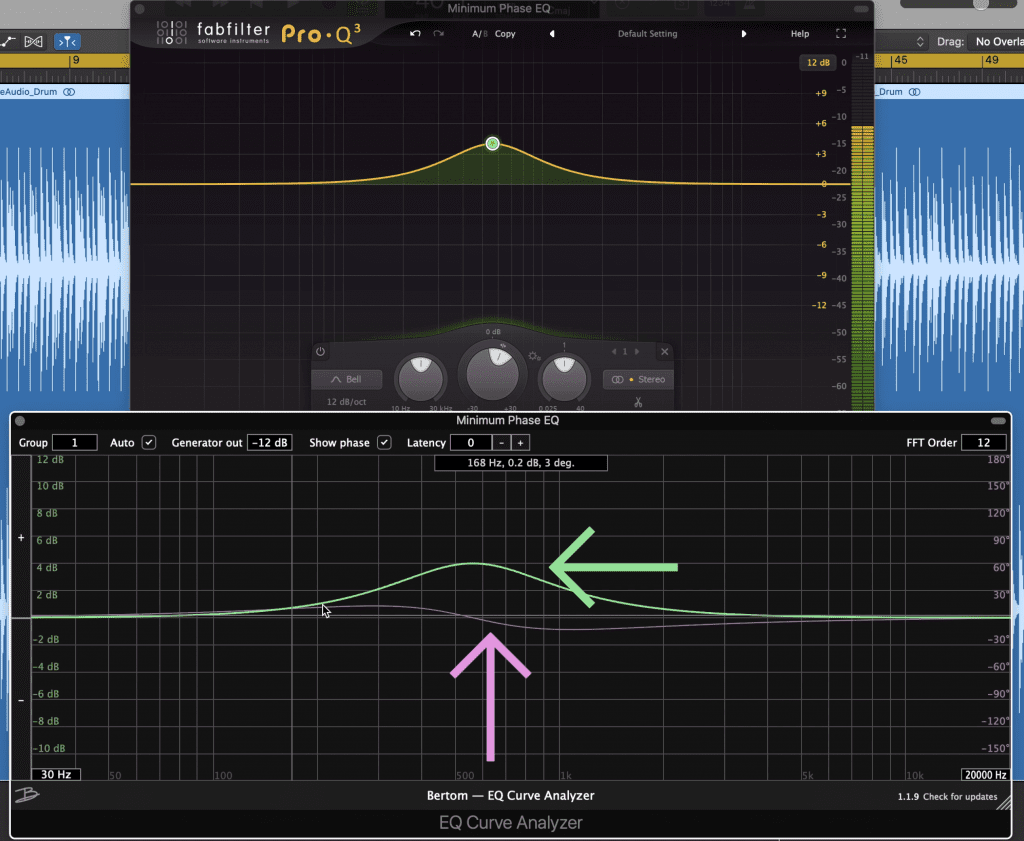
Notice that the green curve matches, but the pink which represents phase does not match.
We can observe that the green line matches that of our EQ, but the pink bar which represents the signal’s phase shifts away from a 0-degree phase, and we can observe to what extent this happens by looking at the degrees on the right side of the analyzer.
The greater we amplify this band, the larger this phase discrepancy becomes. Notice that the only point that is in phase, is the center of the band - but the frequencies around this center are pushed out of phase.
This becomes even worse when we start to affect the low-frequency range, especially when we create a high-pass filter.
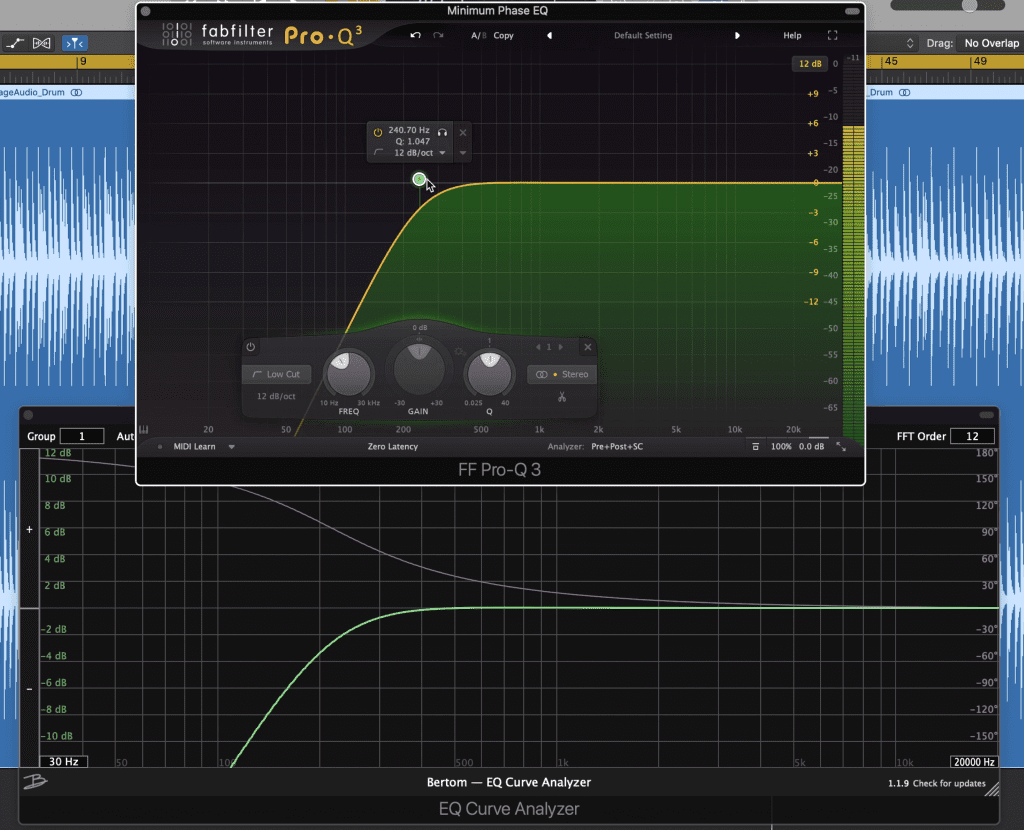
This phase inconsistency is made worse when using a low-cut or high-pass filter.
Now, what isn’t shown here in this analyzer is the aftermath of these phase changes. Because the phase of these frequencies is changing, we’re getting constructive and destructive interference, which ultimately changes the amplitude of our frequencies in unexpected ways.
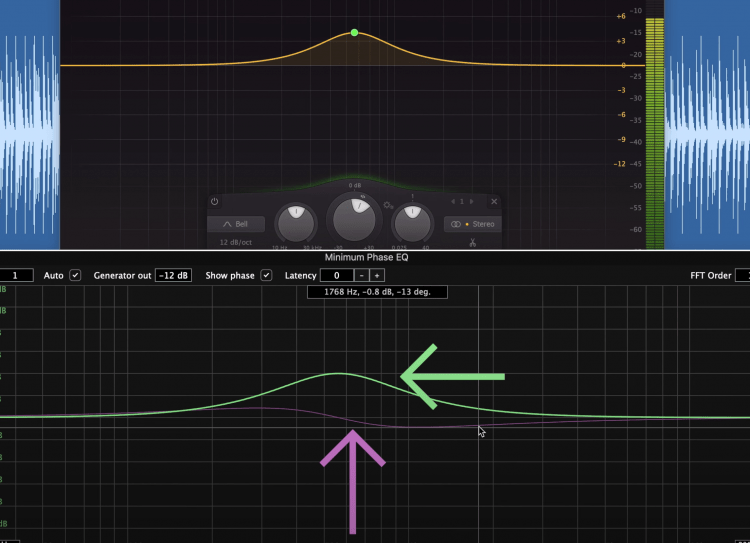
Notice that the great the EQ change, the larger the phase discrepancy.
The worse the phase shift, the more of this strange interference will occur , and the more our EQ curve won’t accurately represent the actual changes we are trying to make to the frequency spectrum.
So, how do we fix this? The answer is to have all samples delayed the same amount of time regardless of what changes are being made.
This is called Linear Phase.
To learn more about the equalizer used here, check out this video:
What is Linear Phase Equalization?
Linear phase equalization is created by delaying all filters in an FFT equalizer by a set equal amount. By delaying all of the filters equally, time discrepancies cannot occur amongst the various filters, in turn reducing phase interference; this all occurs at the expense of greater latency.
Despite the greater latency, less phase cancellation is an important part of mastering, as it results in much more accurate equalization.
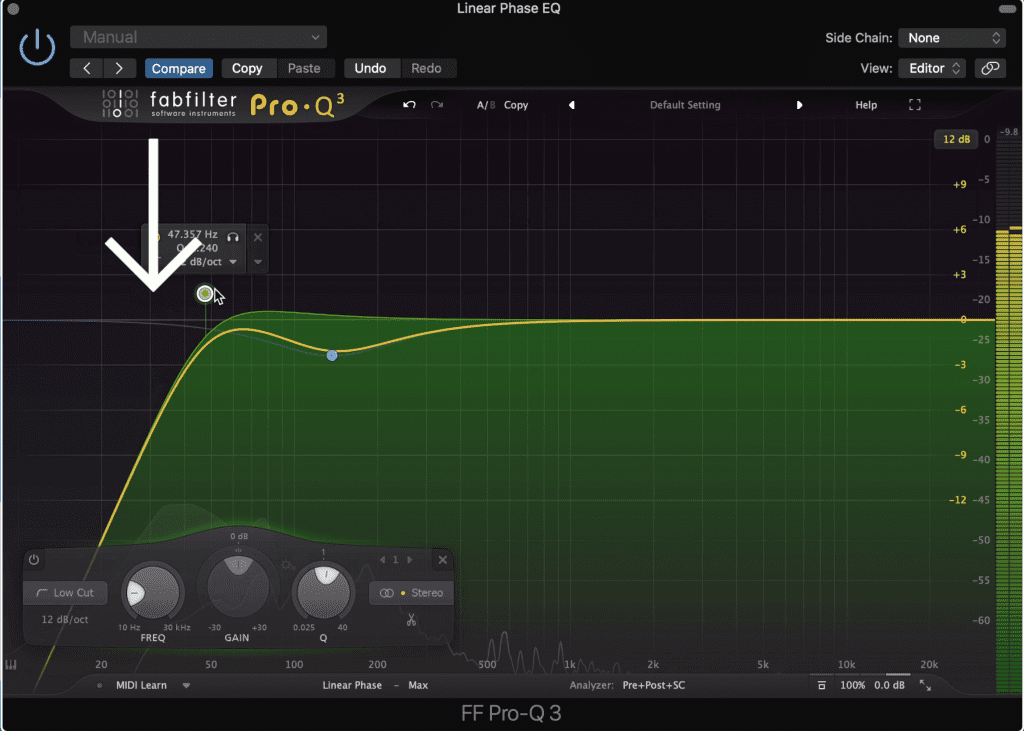
Linear phase is particularly helpful for accurate low-level equalization.
When we increase the linear phase setting from say, low to medium and so on, what we’re doing is increasing the set amount of delay that each individual band has to alter the signal.
In theory, the longer the delay or latency, the less phase interference.
As we covered earlier, phase cancellation and interference play a more significant role in the low-frequency range - so the higher the linear phase setting, the more accurate any equalization to the low frequencies will be.
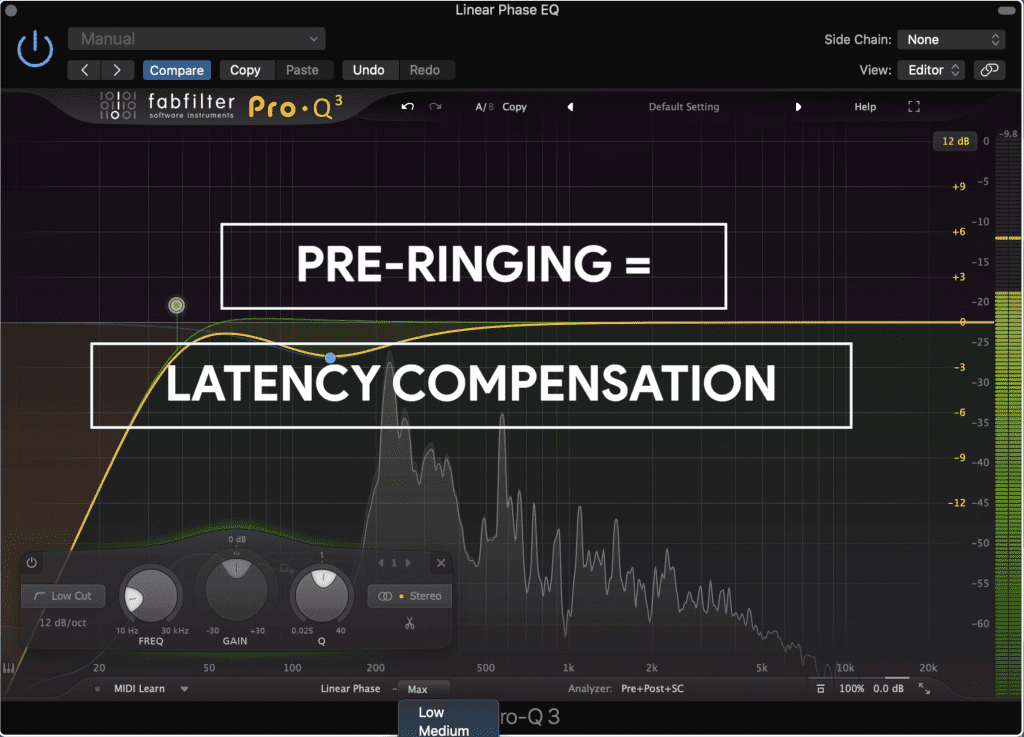
Because linear phase equalizers compensate for latency, this can affect transients in a negative way.
There is one issue that can be caused by linear-phase equalization, and that’s called pre-ringing.
Pre-ringing is caused by a linear phase processor compensating for the latency it causes, in turn shifting the signal further back in time. When this happens the transients of a signal can be mildly altered, resulting in less impact.
This effect becomes more aggressive the higher the latency, so keep an ear out for it when using higher linear phase settings.
How Equalization Can Cause the Haas or Precedence Effect
Aside from causing destructive and constructive interference, and altering frequency response in unwanted and unexpected ways, there is one more really interesting thing that can occur from using equalization.
When we use a minimum phase equalizer or a zero-latency equalizer we have the potential to create what’s known as the Haas effect.
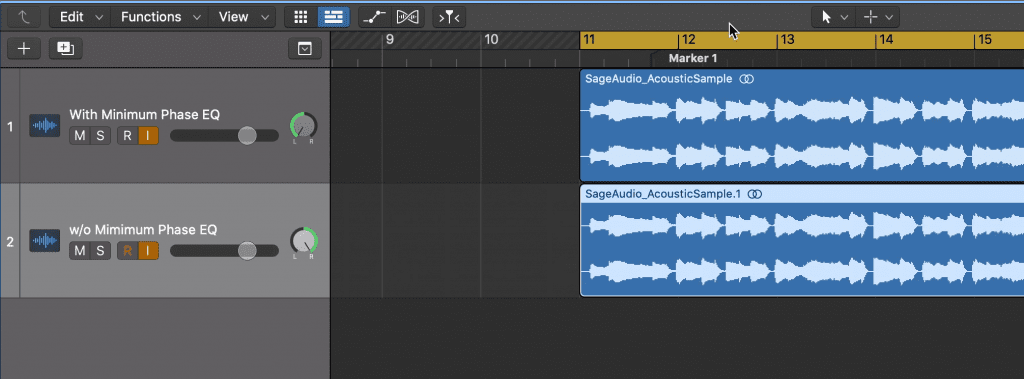
Here we have 2 identical tracks panned hard left and right. One has an EQ, the other does not.
The Haas or Precedence effect occurs when 2 identical signals are played to the left and right ear, with 1 signal delayed slightly.
The signal that arrives first gives the listener a locational cue, in turn making the listening think that the sound is coming from that direction.
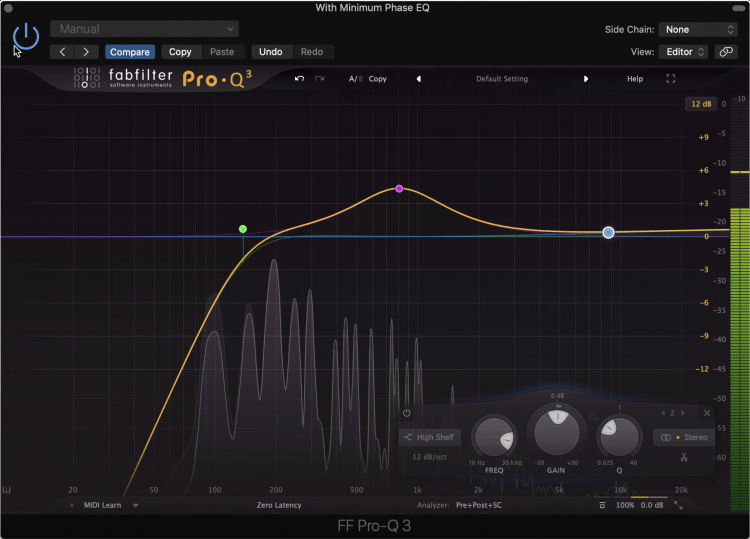
When played back, the sound will seem to come from the direction which does not have the EQ on it.
Following this thought,if we had 2 identical signals panned hard left and right, say an acoustic guitar, and if we used zero-latency equalization on one of them but not the other, we’d shift the phase of that channel.
As a result, the signal could be delayed slightly, causing one channel to drive to the listener first, and in turn, create the Haas effect.
Conclusion
Although there are some clear advantages to using linear phase equalization, it doesn’t mean it’s always the better choice.
Sometimes a little phase cancellation can be beneficial and augment certain pleasant-sounding aspects of the frequency spectrum.
With that in mind, you need to use your ears when determining which setting is right for what you’re working on.
If you’re an artist or engineer, and you have a mix that you’d like to hear mastered, send it to us here:
We’ll master it for you and send you a free mastered sample to review.